【受験数学】立体の体積の求め方を徹底解説！【微分・積分】（例題つき）

今回は、受験数学の微分・積分の分野から立体の体積の求め方について徹底的に解説していきます。

立体の体積については、回転体の体積についての公式を覚えているだけで、回転体以外の体積の求め方がわからなかったり、回転体であっても見たことのないような難易度の高い問題になると途端に解けないという受験生は多いのではないでしょうか。

しかし実は、立体の体積の問題は回転体やその他に限らず共通の方法で解くことができます。

今回は体積を求める一般的な方法を例題を用いて解説していきます！

例題
立体の体積の求め方
例題を用いた解説
まとめ

例題

(例題)
$xyz$ 空間に一辺の長さが $1$ の正四面体 $ABCD$ がある。4つの頂点の座標はそれぞれ
$A\biggl(-\cfrac{1}{2}, 0, 0 \biggr), \quad B\biggl(\cfrac{1}{2}, 0, 0 \biggr), \quad C\biggl(0, \cfrac{\sqrt{3}}{2}, 0 \biggr), \quad D\biggl(0, \cfrac{\sqrt{3}}{6}, \cfrac{\sqrt{6}}{3} \biggr)$
である。
このとき、正四面体 $ABCD$ を $z$ 軸の周りに一回転させてできる立体の体積を求めよ。

この例題では各頂点の座標を問題文で与えていますが、入試問題ではこれらも自分で求めなければならないことが多いです。

（＊これらを求めるためには、座標幾何やベクトルを用いることがほとんどですが、今回はあくまで体積を求める方法に絞って解説するため問題文中に座標を与えました。

この部分についてはまた別の機会に記事を書きたいと思います！）

立体の体積の求め方

立体の体積を求める方法は以下の4ステップで手順化することができます！

(立体の体積の求め方)

積分を行う軸を決める
上記の軸に垂直な平面での立体の断面を考える
上記の断面の面積を求める
断面積を積分して立体の体積を求める

体積を求める方法は、実はこの4ステップだけです。

ここからは上で書いた例題を用いて、それぞれのステップについて具体的な計算方法を解説していきます。

例題を用いた解説

それではStep1から手順を追っていきましょう！

Step1) 積分を行う軸を決める

このステップでは積分を行う軸を決めましょう。

ほとんどの場合は $x軸、y軸、z軸$ のいずれかの軸で計算することになりますが、難易度の高い問題ではその他の軸を選ぶこともあります（例えば斜軸回転など）。

また、この段階で選んだ軸によって、後続の計算量が変わってくるので慎重に選びましょう！

今回は $z$ 軸回転の問題なので、 $z$ 軸を選んでおけば問題ありません！

f:id:hmorinari:20190208214113p:plain

これでStep1は完了です。

次のステップに進みましょう！

Step2) 軸に垂直な平面での断面を考える

このステップでは軸に垂直な平面で、立体を切ったときの断面について考えていきます。

今回、軸は $z$ 軸を選んだので $z$ 軸に垂直な平面 $z = t$ での断面を考えましょう。

回転させた後の立体の断面を最初から考えるのは難しいので、まずは回転させる前の断面から考えていくのがセオリーです。

正四面体を、平面 $z = t$ で切った断面は下図のような三角形になります。

f:id:hmorinari:20190208214426p:plain

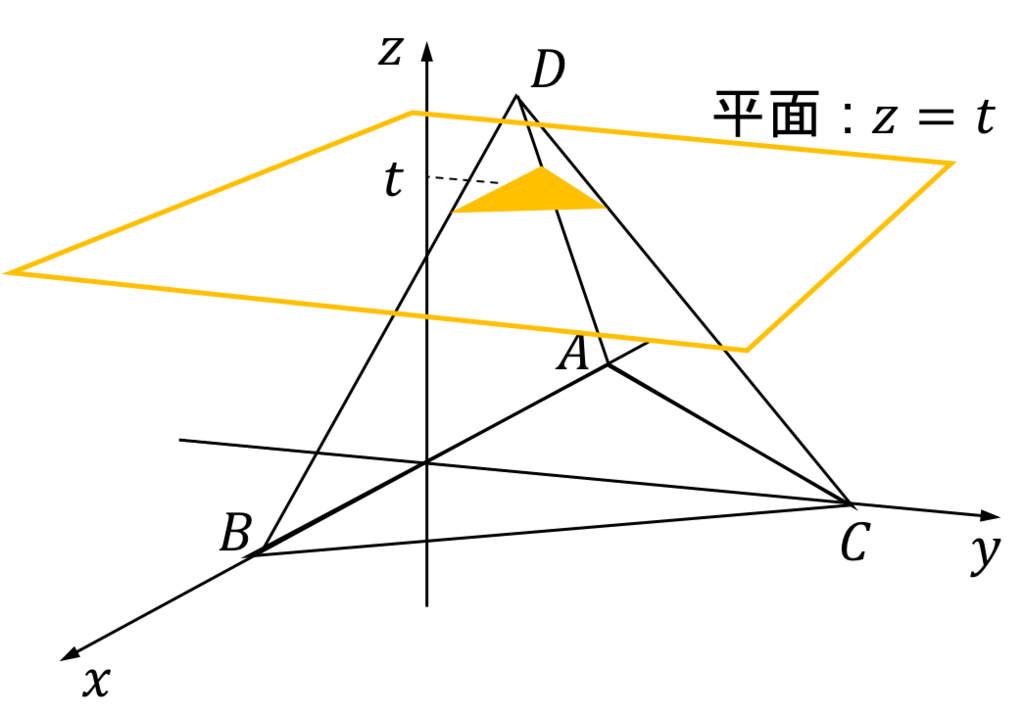
ではまず、四面体の各辺と平面 $z = t$ の交点の座標を求めていきましょう！

交点の座標を求めるには、図形的な性質に注目しても良いですが、座標幾何やベクトルを用いることが多いです。

ここではベクトルを用いて求めていきましょう。

例えば辺 $AD$ と平面 $z = t$ の交点を $A'$ とし、 $\overrightarrow{AA'} = k \overrightarrow{AD}$ としましょう。

そうするとまず、 $\overrightarrow{AD} = \biggl( \cfrac{1}{2}, \cfrac{\sqrt{3}}{6}, \cfrac{\sqrt{6}}{3} \biggr)$ なので、 $\overrightarrow{AA'} = \biggl(\cfrac{k}{2}, \cfrac{\sqrt{3}}{6} k, \cfrac{\sqrt{6}}{3}k \biggr)$ です。

従って $\overrightarrow{OA'} = \overrightarrow{OA} + \overrightarrow{AA'}$ なので、 $\overrightarrow{OA'} = \biggl(\cfrac{k - 1}{2}, \cfrac{\sqrt{3}}{6} k, \cfrac{\sqrt{6}}{3}k \biggr)$ となります。

このとき、点 $A'$ は辺 $AD$ と平面 $z = t$ との交点なので当然 $z$ 座標は $t$ です。

つまり、上で求めた $\overrightarrow{OA'}$ の $z$ 成分に注目して $\cfrac{\sqrt{6}}{3} k = t$ とすることができます。

これを用いて全ての座標を $t$ で表すと、

$A' \biggl( \cfrac{\sqrt{6}}{4} t - \cfrac{1}{2}, \,\, \cfrac{\sqrt{2}}{4} t, \,\, t \biggr)$

となります。

同様にして他の交点の座標（ $B', \,\, C'$ とする）も求めると

$B' \biggl( -\cfrac{\sqrt{6}}{4} t + \cfrac{1}{2}, \,\, \cfrac{\sqrt{2}}{4} t, \,\, t \biggr)$

$C' \biggl( 0, \,\, \cfrac{\sqrt{3} - \sqrt{2} t }{2}, \,\, t \biggr)$

と求まります。

これにより三角形 $A'B'C'$ の平面図を描くと下図のようになります。

f:id:hmorinari:20190208221740p:plain

これより、回転体の断面はドーナツ状になっていることがわかりました！

次のステップで、この断面の面積を求めていきましょう！

Step3) 断面積を求める

Step2の考察により、断面の形状はドーナツ状であることがわかりました。

ドーナツ状の領域の面積は外側の円の面積から内側の円の面積を引くことで求めます。

それぞれ円の面積を求める必要があるので、まずは半径 $R, r$ を求めておきましょう。

$R$ は $C'$ の $y$ 座標に一致するので、

$R = \cfrac{\sqrt{3} - \sqrt{2} t }{2}$

です。

また、 $r$ は $A'やB'$ の $y$ 座標に等しいので

$r = \cfrac{\sqrt{2}}{4} t$

です。

従って、この断面の面積 $S(t)$ は

$S(t) = \pi R^2 - \pi r^2 \\ \quad \quad = \pi \biggl( \cfrac{3}{8} t^2 - \cfrac{\sqrt{6}}{2} t + \cfrac{3}{4} \biggr)$

と求めることができます！

これで断面積を求めることができたので最後のステップに進みましょう。

Step4) 断面積を積分して体積を求める

さて、あとは積分を実行して、体積を計算するだけです。

積分の式は

$V = \int_{0}^{\frac{\sqrt{6}}{3}} {S(t)} dt$

です。

積分区間について、少し補足説明をしておきます。

積分区間は体積を求めたい立体が存在している範囲にすることになります。

今回は $z$ 軸に垂直な平面 $z = t$ が、立体と交点を持つ範囲を考えれば良いことになりますが、元の四面体が $z$ 軸方向で考えると $0 \leqq z \leqq \cfrac{\sqrt{6}}{3}$ の範囲に存在していることから、この範囲を積分区間とすれば良いのです。

さて、積分の式を立式することができました。

被積分関数も今回はただの二次関数なので積分計算も悩むことなく進めることができると思います。

では計算していきましょう。

$V = \int_{0}^{\frac{\sqrt{6}}{3}} {S(t)} dt \\ \quad = \int_{0}^{\frac{\sqrt{6}}{3}} {\pi \biggl( \cfrac{3}{8}t^2 - \cfrac{\sqrt{6}}{2} t + \cfrac{3}{4} \biggr)} dt \\ \quad = \left[ \pi \biggl( \cfrac{1}{8}t^3 - \cfrac{\sqrt{6}}{4}t^2 + \cfrac{3}{4} t \biggr) \right]_{0}^{\frac{\sqrt{6}}{3}} \\ \quad = \cfrac{\sqrt{6}}{9} \pi$